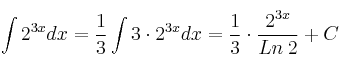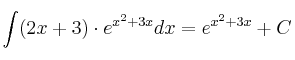INTRODUCCIÓN
APRENDIZAJE ESPERADO (SEGUNDO PARCIAL):
Encuentra la antiderivada de funciones elementales (polinomiales).Reconoce el significado de la integral indefinida con el área bajo la curva
Descubre relaciones inversas entre derivación e integración: '' Si de una función se obtiene su derivada, que obtengo si de esa derivada encuentro su antiderivada''
Interpreta, por extensión o generalización, la integral indefinida de funciones polinomiales y trigonométricas básicas ( inmediatas ).
APRENDIZAJE ESPERADO ( PRIMER PARCIAL ):
Calcula en área bajo la curva por aproximaciones, de una función polinomial, exponencial y trigonometrica en la que indentifica y aplica uno de los métodos por rectángulos y triángulos; analiza los resultados y argumenta la solución obtenida por el método seleccionado.
PRIMER PARCIAL:
EJERCICIOS Y EJEMPLOS RESUELTOS:
ÁREA BAJO LA CURVA CON RECTÁNGULOS ( POR DEFECTO Y EXCESO):
Las integrales formalizan el concepto de área de una manera sencilla e intuitiva. Podemos obtener
aproximaciones de esta área mediante diversos procedimientos. Hace más de 2.000 años, los griegos
desarrollaron el Método de Exhaución para el cálculo de áreas. Este método consiste en ir inscribiendo
en la región cuya área se quiere calcular, regiones poligonales que la aproximan y cuya área seamos capaces
de calcular. Arquímedes usó este método para calcular el área encerrada bajo un segmento de parábola.
Veamos un ejemplo. Calculemos el área del recinto plano limitado por el eje de abscisas, la gráfica de la función y = x2 y las rectas x = 0 y x = 1.
Para cada número natural n dividimos el segmento [0,1] en n partes iguales de longitud 1/n. Sobre cada una de esas partes construimos un rectángulo con la altura de la ordenada máxima (rectángulo superior, por exceso o circunscrito) o bien podemos proceder con la altura de la ordenada mínima (rectángulo inferior, por defecto o inscrito), a medida que aumentemos el valor de n, los rectángulos cubrirán de manera más fidedigna el área bajo la curva, y el valor real del área se encontrará entre los valores por defecto y por exceso de las sumas de las áreas de los rectángulos calculados (Sumas de Riemann).
ÁREA BAJO LA CURVA CON TRAPECIOS
PARA DETERMINAR EL ÁREA DE UNA FIGURA GEOMÉTRICA ES NECESARIO EFECTUAR
OPERACIONES YA CONOCIDAS. SIN EMBARGO, CUANDO SE DESEA CALCULA EL ÁREA BAJO LA
CURVA DE UNA FUNCIÓN O UN CONJUNTO DISCRETO DE DATOS EL CÁLCULO SE PUEDE
COMPLICAR MUCHO. CONSIDEREMOS UN CASO SENCILLO, EL ÁREA BAJO UNA CONSTANTE, COMO EN LA FIGURA 1.
EN LA FIGURA SE HA REPRESENTADO A LA FUNCIÓN CONSTANTE (f(x) = y = h) Y SE DESEA CALCULAR EL ÁREA BAJO LA CURVA EN EL INTERVALO (a, b).
Figura 1.
ES FÁCIL NOTAR QUE SE TRATA DE UN RECTÁNGULO Y QUE CONOCEMOS EL ÁREA DEFINIDA DENTRO DEL RECTÁNGULO.
LA LONGITUD DE LA BASE (b−a) MULTIPLICADA POR LA ALTURA, h, DEL RECTÁNGULO DA COMO RESULTADO EL ÁREA DEL MISMO: (b−a) x h = A.
CONSIDEREMOS AHORA OTRA FUNCIÓN, POR EJEMPLO UNA RECTA QUE PASA A TRAVÉS DEL ORIGEN DEL SISTEMA DE COORDENADAS: f(x) = c x.
COMO PUEDE OBSERVARSE, ES CLARO QUE EL ÁREA QUE SE BUSCA ES EQUIVALENTE A LA DE UN TRIÁNGULO RECTÁNGULO, POR LO QUE EL ÁREA ES [(b−a) x cb]/2 = A O, COMO SUELE HACERSE EN LA GEOMETRÍA, A = (BASE x ALTURA) /2. COMO PUEDE OBSERVARSE, EL ÁREA BAJO LA CURVA (RECTA) SE CALCULA CON FACILIDAD.
Figura 2.
COMO SIGUIENTE EJEMPLO SE TIENE A UNA RECTA QUE NO PASA A TRAVÉS DEL ORIGEN DEL SISTEMA DE REFERENCIA. EN ESTE CASO, EL ÁREA BAJO LA CURVA ES UN TRAPECIO, COMO SE VE EN LA FIGURA 3,POR LO QUE EL ÁREA ES (b−a) x [f(a)+f(b)]/2.
Figura 3.
HASTA AQUÍ, HA SIDO SENCILLO CALCULAR EL ÁREA BAJO LA CURVA, PUES EL CÁLCULO SE HA REDUCIDO A CONSIDERAR FIGURAS GEOMÉTRICAS CONOCIDAS. CUANDO LA FUNCIÓN DIFIERE DE LA DE UNA RECTA, EL CÁLCULO DEL ÁREA BAJO LA CURVA ES MÁS COMPLICADO Y SE REQUIERE DE LAS SUMAS DE RIEMANN PARA EFECTUAR DICHO CÁLCULO. LAS SUMAS DE RIEMANN NOS CONDUCIRÁN AL CONCEPTO DE LA INTEGRAL DEFINIDA COMO EL ÁREA BAJO LA CURVA EN UN INTERVALO DADO
EN LA FIGURA 4 SE OBSERVA UNA CURVA QUE NO ES UNA RECTA, POR LO QUE HACER APROXIMACIONES USANDO TRAPECIOS ES LO RECOMENDABLE.
Figura 4.

COMO EN LOS CASOS ANTERIORES, DEBE ESTAR DEFINIDO UN INTERVALO EN EL QUE SE DESEA HALLAR EL ÁREA BAJO LA CURVA DE LA FUNCIÓN ESPECIFICADA.
SEA EL INTERVALO (b−a) EN EL QUE SE EFECTUARÁ EL CÁLCULO DEL ÁREA BAJO LA CURVA.
HAGAMOS UNA PARTICIÓN REGULAR DE DICHO INTERVALO, PARA OBTENER EL MISMO NÚMERO DE TRAPECIOS CUYA BASE SEA LA MISMA PARA TODOS. SI DESEAMOS QUE LA PARTICIÓN SEA DE TAMAÑO 10, ENTONCES, LA ANCHURA DE CADA TRAPECIO SERÁ ∆x=(b−a)/10.
LUEGO, ETIQUETEMOS A CADA SEGMENTO DE LA PARTICIÓN EMPEZANDO CON x0 =a, Y x i =x0 +i ∆x, con i=1, 2, ..., 10 (el tamaño de la partición).
A CONTINUACIÓN, SE EVALÚA f(x i ) PARA DEFINIR A CADA TRAPECIO QUE SE USARÁ EN EL CÁLCULO, DE MODO QUE EL ÁREA BAJO LA CURVA SE PODRÁ APROXIMAR SUMANDO LAS ÁREAS DE TODOS LOS TRAPECIOS CONSTRUIDOS DE ESTE MODO.
FINALMENTE, EL ÁREA SE CALCULA DE ACUERDO CON

Y CALCULEMOS EL ÁREA BAJO LA CURVA
PARA ENTENDER MEJOR EL TEMA TE RECOMENDAMOS ESTE VÍDEO:
SEGUNDO PARCIAL:
ANTIDERIVADALa antiderivada es la función que resulta del proceso inverso de la derivación, es decir, consiste en encontrar una función que, al ser derivada produce la función dada.
La antiderivada también se conoce como la primitiva o la integral indefinida se expresa de la siguiente manera: en donde f(x) es el integrando; dx la variable de integración o diferencial de x y C es la constante de integración.
EJEMPLOS:
1-. Si f(x) = 3x2, entoces, F(x)=3, es una antiderivada de f(x). Observe que no existe una derivada unica para cada función. Por ejemplo, si G(x)=x3 + 5, entonces es otra antiderivada de f(x).
2-.
Se toma el exponente y se le suma uno y eso se divide entre el exponente mas uno
INTEGRAL INDEFINIDA
El proceso de encontrar las antiderivadas suele recibir el nombre de integración. Y la familia de funciones obtenidas mediante ese proceso se llama integral indefinida.
La notación:
∫ f (x) dx
se emplea con frecuencia para indicar la integral indefinida de la función f. El símbolo ∫ es
el signo de integral; f es el integrando, o sea la función cuya integral indefinida se desea
obtener; y dx, tal como se considera aquí, denota la variable respecto de la cual se realiza
el proceso de integración. Dos descripciones verbales del proceso indicadas por la ecuación son “integrar la función f respecto de la variable x” y “encontrar la integral indefinida de f respecto de x”.
La Integral Indefinida se representa por: ∫ f (x) dx
- Se lee: integral de x diferencial de x
- ∫ es el signo de integración
- F(x) es el integrando o función a integrar
- Dx es diferencial de x, e indica cuál es la variable de la función que se integra
- C es la constante de integración y puede tomar cualquier valor numérico real
- Si F(x) es una primitiva de f(x) se tiene que:
- ∫ f (x) dx = F(x) + C
- Para comprobar que la primitiva una función es correcta basta con derivar
EJEMPLO:
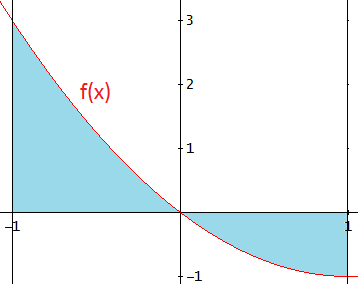
1.Calcular el área de la región delimitada por la gráfica de la función
y las rectas verticales
Como el eje OX divide la región en otras dos (una sobre el eje y otra bajo éste), tenemos que calcular dos integrales. El resultado de la integral correspondiente al área que está por debajo será negativo, por lo que tenemos que cambiar el signo (o escribir el valor absoluto).
Los intervalos de x de las regiones son:
Nota: el extremo 0 se calcula resolviendo la ecuación
Estos intervalos son los extremos de las integrales.
La integral indefinida de f es
Calculamos las áreas calculando las integrales definidas aplicando la Regla de Barrow:
![calculamos las integrales definidas de x^2-2x en
los intervalos [-1,0] y [1,0]
integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos. Áreas entre gráficas de funciones. Introducción a la integral impropia de Riemann](https://www.matesfacil.com/primitivas/ReAr1-4.jpg) El área es la suma del valor absoluto de los resultados obtenidos:
El área es la suma del valor absoluto de los resultados obtenidos:
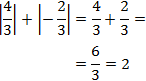
Los intervalos de x de las regiones son:
La integral indefinida de f es
![calculamos las integrales definidas de x^2-2x en
los intervalos [-1,0] y [1,0]
integrales definidas: cálculo de áreas (regiones) del plano: ejercicios resueltos. Áreas entre gráficas de funciones. Introducción a la integral impropia de Riemann](https://www.matesfacil.com/primitivas/ReAr1-4.jpg)
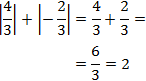
INTEGRAL EXPONENCIAL:
Se llama función exponencial de base a aquella cuya forma genérica es f (x) = ax, siendo a un número positivo distinto de 1. Por su propia definición, toda función exponencial tiene por dominio de definición el conjunto de los números reales R.
La función exponencial puede considerarse como la inversa de la función logarítmica, por cuanto se cumple que:

PROPIEDADES DE LAS FUNCIONES EXPONENCIALES:
Para toda función exponencial de la forma f(x) = ax, se cumplen las siguientes propiedades generales:
- La función aplicada al valor cero es siempre igual a 1:f (0) = a0 = 1.
- La función exponencial de 1 es siempre igual a la base:f (1) = a1 = a.
- La función exponencial de una suma de valores es igual al producto de la aplicación de dicha función aplicada a cada valor por separado.f (x + x?) = ax+x? = ax × ax? = f (x) × f (x?).
- La función exponencial de una resta es igual al cociente de su aplicación al minuendo dividida por la función del sustraendo:f (x - x?) = ax-x? = ax/ax? = f (x)/f (x?).
EJEMPLOS:
1.- Un ejemplo de ecuación exponencial sería ax = b.
Para resolver estas ecuaciones se suelen utilizar dos métodos alternativos:
- Igualación de la base: consiste en aplicar las propiedades de las potencias para lograr que en los dos miembros de la ecuación aparezca una misma base elevada a distintos exponentes:Ax = Ay.En tales condiciones, la resolución de la ecuación proseguiría a partir de la igualdad x = y.
- Cambio de variable: consiste en sustituir todas las potencias que figuran en la ecuación por potencias de una nueva variable, convirtiendo la ecuación original en otra más fácil de resolver.22x - 3 × 2x - 4 = 0
t2 - 3t - 4 = 0
PARA ENTENDER MEJOR LOS TEMAS TE RECOMENDAMOS ESTE VÍDEO:
Te podría interesar:
SumasDeReihmanTERCER PARCIAL:
INTEGRALES INDEFINIDAS:
La idea de la integral indefinida supuso un paso más en el camino de la abstracción emprendido por las matemáticas modernas. Con ella, la integral dejó de referirse únicamente a un modo de determinar las áreas que forman curvas y rectas para asumir la condición de función en sí, susceptible de formar parte de ecuaciones y descripciones de modelos en el gran marco de las teorías del análisis matemático.
Primitivas
Dada una función f (x), se dice que la función F (x) es primitiva de ella si se verifica que F¿ (x) = f (x). La operación consistente en obtener la primitiva de una función dada se denomina integración, que es la inversa de la derivación.
De esta definición se desprende que la función f (x) posee infinitas primitivas, ya que si F (x) es primhtiva de f (x), también lo será cualquier otra función definida como G (x) = F (x) + C, siendo C un valor constante.
El conjunto de todas las primitivas de una función f (x) dada se denomina integral indefinida de la función, y se denota genéricamente como:
Las primitivas de una función forman una familia de curvas desplazadas verticalmente unas de otras. Así, la función f (x) = x tiene infinitas primitivas que difieren en una constante, tal como se muestra a la derecha.
Propiedades de las primitivas
Aplicando las propiedades de la derivación (ver t43), es posible determinar algunas propiedades comunes de la integración. Las siguientes propiedades de linealidad sirven para descomponer integrales complicadas en otras más sencillas:
- La integral de la suma (o diferencia) de dos funciones es igual a la suma (o diferencia) de las integrales de cada una de ellas.
- La integral del producto de una constante por una función es igual al producto de la constante por la integral de la función.
Tabla de integrales inmediatas
En la tabla siguiente se resumen las reglas de integración de algunas funciones comunes. En general, se llama integrales inmediatas a las que se deducen directamente de esta tabla y de las propiedades de linealidad de la integración.
CAMBIO DE VARIABLES:
Ejemplo: resolver .
Solución: Primero hay que observar que la ecuación es equivalente a , lo cual sugiere el cambio de variable
, y la ecuación se transforma en una cuadrática --y ya se sabe cómo resolver éstas.
La ecuación cuadrática también se puede resolver con cambio de variable. Consideremos la ecuación de segundo grado . Haciendo el cambio de variable , se puede obligar a que el coeficiente de en la cuadrática que resulte sea cero --de manera que la ecuación se simplifique a una de la forma
. (En la práctica, a veces, este método se simplifica apelando a las fórmulas de Vieta: el coeficiente de la x es la suma de las raíces cambiada de signo.)
Ejemplo: Resolver la ecuación
Solución: Como las raíces, digamos
suman -10, ello sugiere el cambio de variable . Este cambio de variable resulta en la ecuación simplificada
. (La cuadrática más fácil de resolver, como ya lo sabe el lector.)
Es una técnica para resolver ecuaciones (o sistemas de ecuaciones). Su objetivo es simplificar la ecuación al plantearla en la nueva variable y facilitar así su resolución. Una vez resuelta la ecuación, se deshace el cambio de variable, es decir, se regresa a la variable original.
Procedimiento a seguir:
- Decidir el cambio de variable a usar (
x - Calcular
dt x dx - Sustituir
t x - Calcular la integral indefinida en función de t
- Volver a sustituir las
t x x
Integrales definidas por cambio de variable
Procedimiento a seguir:
- Decidir el cambio de variable a usar (
x - Calcular
dt dx. - Sustituir
t dt x. - Calcular la integral indefinida en función de t
- Volver a sustituir las
t x.
INTEGRACIÓN POR PARTES:
Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
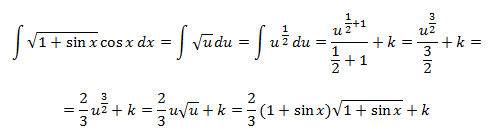
Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).
Aunque se trata de un método simple, hay que aplicarlo correctamente.
Método:
- El integrando debe ser un producto de dos factores.
- Uno de los factores será u y el otro será dv.
- Se calcula du derivando u y se calcula v integrando dv.
- Se aplica la fórmula.
CONSEJOS:
Escoger adecuadamente u y dv:
Una mala elección puede complicar más el integrando.
Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo x3). Si consideramos dv = x3. Entonces, integrando tendremos que v = x4/4, con lo que hemos aumentado el grado del exponente y esto suele suponer un paso atrás.
Normalmente, se escogen los monomios como u para reducir su exponente al derivarlos. Cuando el exponente es 0, el monomio es igual a 1 y el integrando es más fácil.
Algo parecido ocurre con las fracciones (como 1/x). Si consideramos dv = 1/x, tendremos v = log|x| y, probablemente, obtendremos una integral más difícil.
Como norma general, llamaremos u a las potencias y logaritmos y dv a las exponenciales, fracciones y funciones trigonométricas.
No cambiar la elección:
A veces tenemos que aplicar el método más de una vez para calcular una misma integral.
En estas integrales, al aplicar el método por n-ésima vez, tenemos que llamar u al resultado du del paso anterior y dv al resultado v. Si no lo hacemos así, como escoger una opción u otra supone integrar o derivar, estaremos deshaciendo el paso anterior y no avanzaremos.
Integrales cíclicas:
En ocasiones, tras aplicar dos veces integración por partes, tenemos que despejar la propia integral de la igualdad obtenida para poder calcularla.
EJEMPLOS Y EJERCICIOS RESUELTOS
(PARA ENTENDER MEJOR LOS TEMAS) :